Thứ Ba, 10 tháng 3, 2015

Bài học từ Thập Giá

TRẦM THIÊN THU (Chuyển ngữ từ Beliefnet.com)
Thánh Mátthêu giải thích rằng Chúa Giêsu biết Ngài phải làm gì để cứu độ nhân loại: “Người phải đi Giêrusalem, phải chịu nhiều đau khổ do các kỳ mục, các thượng tế và kinh sư gây ra, rồi bị giết chết, và ngày thứ ba sẽ sống lại” (Mt 16:21).
Có nhiều bài học Chúa Giêsu dạy chúng ta khi Ngài bị treo trên Thập Giá. Đây là vài bài học nổi bật:
HÃY TẬP TRUNG
Chúa Giêsu dạy chúng ta tập trung vào lời mời gọi và ý muốn của Thiên Chúa dành cho cuộc đời chúng ta, mặc dù có nhiều đau khổ.
HÃY TIN TƯỞNG
Tin tưởng và phó thác cho Thiên Chúa không là điều dễ thể hiện. Khi hấp hối trên Thập Giá, Chúa Giêsu cũng run sợ: “Lạy Cha, nếu có thể được, xin cho con khỏi phải uống chén này. Tuy vậy, xin đừng theo ý con, mà xin theo ý Cha. Lạy Cha, nếu con cứ phải uống chén này mà không sao tránh khỏi thì xin vâng Ý Cha (Mt 26:39 và 42).
HÃY CHÂN THẬT
Với nhân tính, Ngài cũng cảm thấy cô đơn tột cùng trong giây phút cuối đời: “Lạy Chúa, lạy Thiên Chúa của con, sao Ngài bỏ rơi con?” (Mt 27:46; Mc 15:34). Nhưng Ngài vẫn xin vâng ý Cha để mọi lời tiên tri nên trọn. Trong mọi hoàn cảnh, chỉ có Thiên Chúa mới có thể giải thoát chúng ta.
HÃY THA THỨ
Trên Thập Giá, Chúa Giêsu đã tha thứ cho những kẻ giết Ngài. Có sự tự do khi chúng ta trao ai đó cho Thiên Chúa, và để Thiên Chúa xử lý. Nếu Ngài đã tha thứ cho kẻ thù, chúng ta cũng có thể tha thứ cho nhau: “Lạy Cha, xin tha cho họ, vì họ không biết việc họ làm” (Lc 23:34).
HÃY KHUYẾN KHÍCH
Hãy khuyến khích người khác, hãy chúc lành cho người lạ. Chúa Giêsu đã tha thứ cho tên cướp bị đóng đinh ở bên Ngài, và cho anh ta vào Nước Trời với Ngài ngay đêm hôm đó. Hãy tín thác vào lòng thương xót của Thiên Chúa, và hãy trở nên ánh sáng cho người khác vì danh Đức Giêsu Kitô.
HÃY CHẾT CHO TỘI LỖI
Thập Giá cho thấy những gì con người có thể làm cho con người. Mọi tội lỗi đã trút lên Chúa Giêsu trong buổi chiều Thứ Sáu Tuần Thánh, buổi chiều định mệnh, và Ngài đã khiêm nhường gánh lấy hình phạt thay cho chúng ta. Con người phải chết về thể lý, nhưng là chết cho tội lỗi của chính mình.

Người đăng: vào lúc Không có nhận xét nào:

Chủ Nhật, 8 tháng 3, 2015

Định lý Fermat lớn

Định lý nhỏ Fermat

Bách khoa toàn thư mở Wikipedia
Định lý nhỏ của Fermat (hay định lý Fermat nhỏ - phân biệt với định lý Fermat lớn) khẳng định rằng nếu p là một số nguyên tố, thì vớisố nguyên a bất kỳ, ap – a sẽ chia hết cho p. Nghĩa là:
a^p \equiv a \pmod{p}\,\!
Một cách phát biểu khác của định lý như sau: nếu p là số nguyên tố và a là số nguyên nguyên tố cùng nhau với p, thì ap-1 - 1 sẽ chia hết cho p. Bằng ký hiệu đồng dư ta có:
a^{p-1} \equiv 1 \pmod{p}\,\!
Cũng có một cách phát biểu khác là: Nếu p là một số nguyên tố và a là số nguyên không chia hết cho p, thì a lũy thừa bậc p-1 có số dư bằng 1 khi chia cho p.
Định lý Fermat nhỏ là cơ sở để kiểm tra tính nguyên tố theo xác suất trong kiểm tra Fermat.

Lịch sử[sửa | sửa mã nguồn]

Pierre de Fermat lần đầu thông báo định lý trong một bức thư đề ngày 18 tháng mười, năm 1640 cho bạn ông là Frénicle de Bessy (theo[1]): p chia hết a^{p-1}-1\, khi p là nguyên tố và a là số nguyên tố cùng nhau với p.
Như thường lệ, Fermat không chứng minh định lý này chỉ thông báo:
Et cette proposition est généralement vraie en toutes progressions et en tous nombres premiers; de quoi je vous envoierois la démonstration, si je n'appréhendois d'être trop long.
(And this proposition is generally true for all progressions and for all prime numbers; the proof of which I would send to you, if I were not afraid to be too long.)
Euler lần đầu tiên công bố một chứng minh vào năm 1736 trong bài báo tựa đề "Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio", nhưng Leibniz đã có chứng minh với ý tưởng tương tự trong bản thảo không được công bố vào khoảng trước năm 1683.
Tên gọi "định lý nhỏ của Fermat" được dùng lần đầu vào năm 1913 trong Zahlentheorie bởi Kurt Hensel:
Für jede endliche Gruppe besteht nun ein Fundamentalsatz, welcher der kleine Fermatsche Satz genannt zu werden pflegt, weil ein ganz spezieller Teil desselben zuerst von Fermat bewiesen worden ist."
(There is a fundamental theorem holding in every finite group, usually called Fermat's little Theorem because Fermat was the first to have proved a very special part of it.)

Lịch sử xa hơn[sửa | sửa mã nguồn]

Một cách độc lập các nhà toán học Trung Quốc đưa ra một giả thuyết (thường gọi là giả thiết Trung Quốc) rằng p\, là một số nguyên tố nếu và chỉ nếu 2^p \equiv 2 \pmod{p}\,. Đúng là nếu p\, là số nguyên tố, thì 2^p \equiv 2 \pmod{p}\,. Đây là trường hợp đặc biệt của định lý nhỏ của Fermat. Tuy thế, điều ngược lại (nếu \,2^p \equiv 2 \pmod{p} thì p\, là số nguyên tố) là sai. Chẳng hạn, 2^{341}\equiv 2 \pmod{341}\,, nhưng 341=11 \times 31 là hợp số (nó là số giả nguyên tố (pseudoprime).

Chứng minh[sửa | sửa mã nguồn]

Fermat phát biểu định lý mà không chứng minh. Xem chi tiết trong Các chứng minh của định lý nhỏ Fermat.

Tổng quát hóa[sửa | sửa mã nguồn]

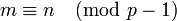Một dạng tổng quát của định lý này là: nếu p là số nguyên tố và m và n là các số nguyên dương thỏa mãn m\equiv n\pmod{p-1}\,, thì \forall a\in\mathbb{Z}: \quad a^m\equiv a^n\pmod{p}..
Định lý Fermat còn được tổng quát hóa bởi Định lý Euler: với modulo n bất kỳ và số nguyên a bất kỳ là số nguyên tố cùng nhau vớí n, ta có
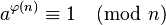
a^{\varphi (n)} \equiv 1 \pmod{n}
trong đó φ(n) là ký hiệu của phi hàm Euler đếm số các số nguyên giữa 1 và n nguyên tố cùng nhau với n. Đây là tổng quát hóa của định lý nhỏ Fermat vì nếu n = p là số nguyên tố thì φ(p) = p − 1.
Tổng quát hơn nữa là Định lý Carmichael.
Một định lý khác tống quát hóa của nó nằm trong các trường hữu hạn.

Số giả nguyên tố

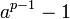Nếu p là hợp số và có số nguyên a sao cho \,a^{p-1} - 1 chia hết cho p, thì p được gọi là số giả nguyên tố cơ sở a. F. Sarrus vào năm1820 đã tìm thấy 341 = 11×31 là số giả nguyên tố đầu tiên,với cơ sở 2.
Một số p là số giả nguyên tố cơ sở a với mọi (a,p)=1 thì được gọi là số Carmichael (chẳng hạn 561).
Người đăng: vào lúc Không có nhận xét nào:
Đăng ký: Bài đăng (Atom)